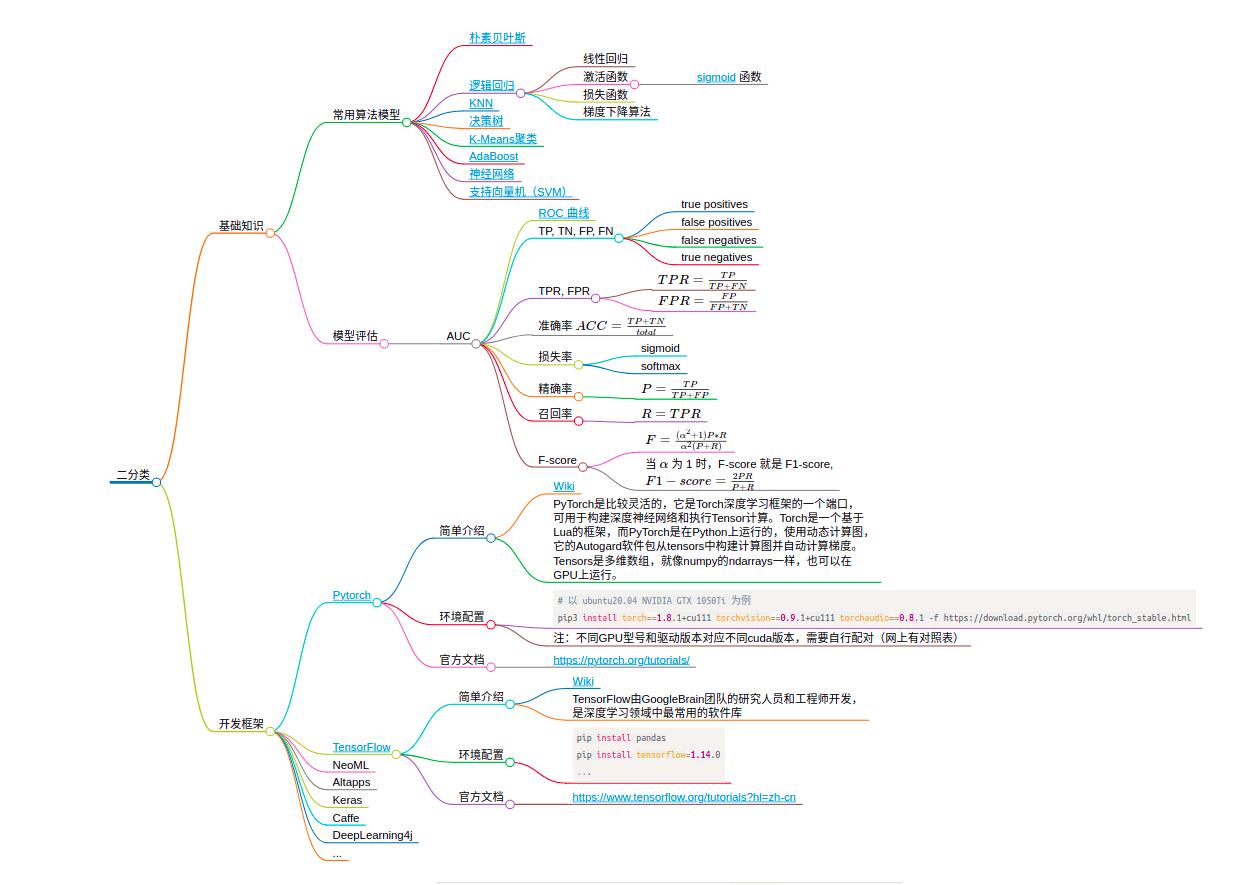
二分类常用的评价指标是 AUC(Area Under Curve),也就是ROC曲线和x轴之间的面积。
1. 什么是ROC曲线(Wiki)
在了解AUC之前首先需要知道ROC曲线。在信号检测理论中,接收者操作特征曲线(receiver operating characteristic curve,即ROC曲线)是一种坐标图式的分析工具,用于 (1) 选择最佳的信号侦测模型、舍弃次佳的模型。 (2) 在同一模型中设定最佳阈值。
在做决策时,ROC分析能不受成本/效益的影响,给出客观中立的建议。
2. 一些术语
| 真实值 | 总数 | |||
|---|---|---|---|---|
| p | n | |||
| 预 测 输 出 | p' | 真阳性 (TP) | 伪阳性 (FP) | P' |
| n' | 伪阴性 (FN) | 真阴性 (TN) | N' | |
| 总数 | P | N | ||
下面所有的内容都是基于此混淆矩阵的。
TP(真阳性)
true positives,即正例被判定为正例的数量
TN(真阴性)
true negatives,即范例被判定为反例的数量
FP(伪阳性)
false positives,即反例被判定为正例的数量
FN(伪阴性)
false negative,即正例被判定为反例的数量
TPR(真阳性率)
true positives rate,又称:命中率 (hit rate)、敏感度(sensitivity)
$ TPR = \frac{TP}{P} = \frac{TP}{TP+FN}$
FPR(伪阳性率)
false positive rate,又称:错误命中率,假警报率 (false alarm rate)
$ FPR = \frac{FP}{N} = {FP}{FP + TN}$
ACC(准确度)
accuracy,(真阳性+真阴性) / 总样本数
$ACC = \frac{TP + TN}{P + N}$
Precision(精确率)
$Precision = \frac{TP}{TP+FP}$ ,即当前划分到正样本类别中,被正确分类的比例。
Recall(召回率)
$Recall = TPR$ ,即所有的正样本类别中,被正确划分到正样本的比例(召回了多少正样本比例)。
Loss (损失率)
待确定
F1-Score
F-Score 是 Precision 和 Recall 的加权调和平均,即
$\frac{1}{F} = \frac{1}{\alpha^2+1}\frac{1}{P}+\frac{\alpha^2}{\alpha^2+1}\frac{1}{R}$
$F=\frac{(\alpha^2+1)P*R}{\alpha^2P+R}$
当 $\alpha=1$ 时,F-Score 就是 F1-Score:
$\frac{1}{F1}=\frac{1}{2}(\frac{1}{P}+\frac{1}{R})$
$ F1=\frac{2PR}{P+R}$
3. ROC空间
ROC空间将伪阳性率(FPR)定义为 X 轴,真阳性率(TPR)定义为 Y 轴。
给定一个二元分类模型和它的阈值,就能从所有样本的(阳性/阴性)真实值和预测值计算出一个 (X=FPR, Y=TPR) 座标点。
从 (0, 0) 到 (1,1) 的对角线将ROC空间划分为左上/右下两个区域,在这条线的以上的点代表了一个好的分类结果(胜过随机分类),而在这条线以下的点代表了差的分类结果(劣于随机分类)。
完美的预测是一个在左上角的点,在ROC空间座标 (0,1)点,X=0 代表着没有伪阳性,Y=1 代表着没有伪阴性(所有的阳性都是真阳性);也就是说,不管分类器输出结果是阳性或阴性,都是100%正确。一个随机的预测会得到位于从 (0, 0) 到 (1, 1) 对角线(也叫无识别率线)上的一个点;最直观的随机预测的例子就是抛硬币。
4. ROC 曲线
上述ROC空间里的单点,是给定分类模型且给定阈值后得出的。但同一个二元分类模型的阈值可能设定为高或低,每种阈值的设定会得出不同的FPR和TPR。
- 将同一模型每个阈值 的 (FPR, TPR) 座标都画在ROC空间里,就成为特定模型的ROC曲线。
5. AUC
ROC曲线下方的面积(英语:Area under the Curve of ROC (AUC ROC)),其意义是:
- 因为是在1x1的方格里求面积,AUC必在0~1之间。
- 假设阈值以上是阳性,以下是阴性;
- 若随机抽取一个阳性样本和一个阴性样本,分类器正确判断阳性样本的值高于阴性样本之几率 。
- 简单说:AUC值越大的分类器,正确率越高。
从AUC判断分类器(预测模型)优劣的标准:
- AUC = 1,是完美分类器,采用这个预测模型时,存在至少一个阈值能得出完美预测。绝大多数预测的场合,不存在完美分类器。
- 0.5 < AUC < 1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
- AUC = 0.5,跟随机猜测一样(例:丢铜板),模型没有预测价值。
- AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
6. AUC 计算方法
二者都是逼近法求近似值
1)梯形法
简单地将每个相邻的点以直线连接,计算连线下方的总面积。因为每一线段下方都是一个梯形,所以叫梯形法。
- 优点:简单,所以常用。
- 缺点:倾向于低估AUC。
2)ROC AUCH法
暂无。
参考:
https://testerhome.com/topics/10527